Sketchy Polytopes | Sketchy Polytopes

Loading [MathJax]/jax/output/HTML-CSS/jax.js

Convex optimization

A fearful sphere, whose center is everywhere

A fearful sphere, whose center is everywhere — In a beautiful article, The Mathematics of Doodling, Ravi Vakil poses two problems:

Accelerated first-order methods for regularization

Accelerated first-order methods for regularization — FISTA

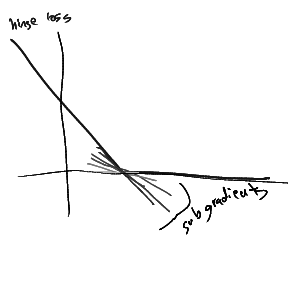
Subgradient

Subgradient — Subgradient generalizes the notion of gradient/derivative and quantifies the rate of change of non-differentiable/non-smooth function ([1], section 8.1 in [2]). For a real-valued function, the

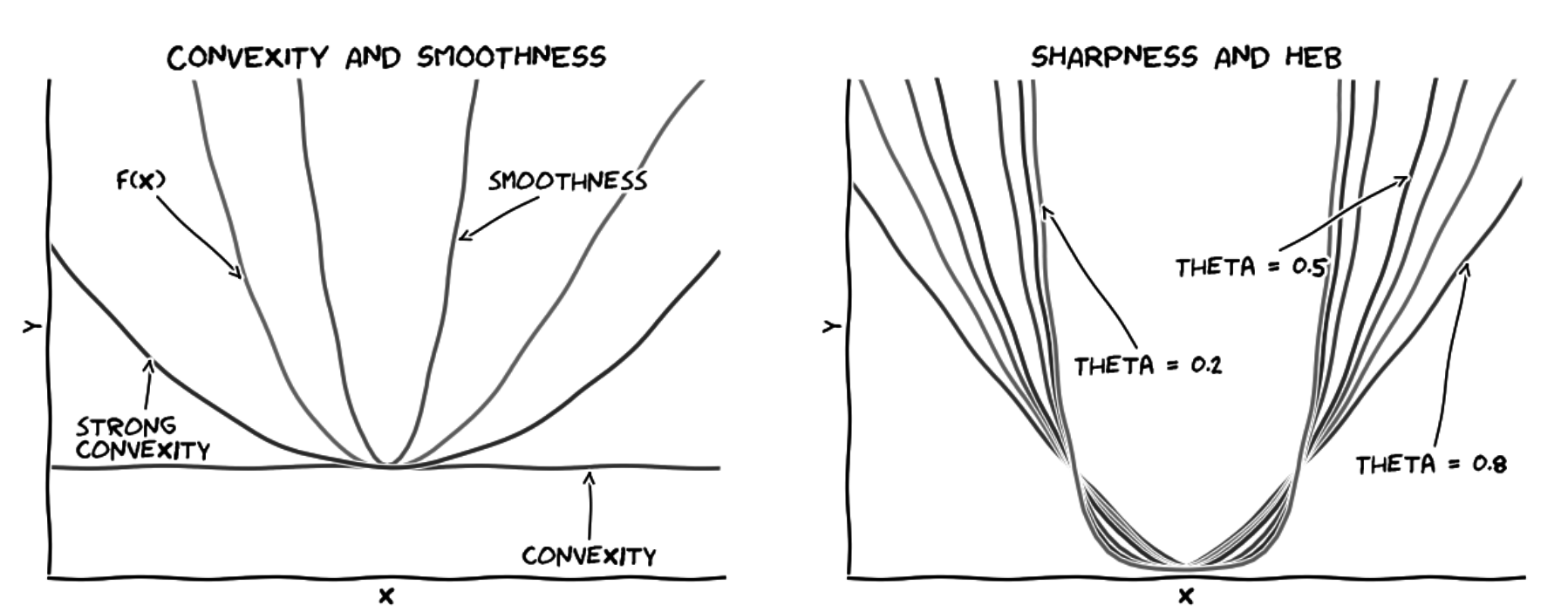
α-strong convexity, β-strong smoothness

α-strong convexity, β-strong smoothness — Strong convexity often allows for optimization algorithms that converge very quickly to an -optimum (rf. FISTA and NESTA). This post will cover some fundamentals of

Obituaries: Harold Kuhn (1925–2014) —

Accelerating first-order methods

Accelerating first-order methods — The lower bound on the oracle complexity of continuously differentiable, -smooth convex function is [Theorem 2.1.6, Nesterov04; Theorem 3.8, Bubeck14; Nesterov08]. General first-order gradient

First-order methods for regularization

First-order methods for regularization — General first-order methods use only the values of objective/constraints and their subgradients to optimize non-smooth (including constrained) function [5]. Such methods that are oblivious to