Accelerated first-order methods for regularization

24 Jul 2014

FISTA

Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) [Beck09] was one of the first algorithms to use Nesterov’s accelerated gradient descent to speed up the convergence of iterative shrinkage-thresholding (ISTA) from $O(\frac{\beta}{\epsilon})$ to $O(\sqrt{\frac{\beta}{\epsilon}})$. The algorithm and proof sketch for in the previous post based were based on [Bubeck14] and [Beck09] so we’ll skip them. Instead give an R implementation and results that compares ISTA and FISTA performance (in terms of number of iterations) for various step sizes (iterations increase and step size decreases).

## ISTA
ista <- function(A, x, beta, iter = 100) {
    ## parameters
    eta <- 1 / beta
    lambda <- 1
    xx <- c(0, 0, 0, 0, 0, 0)
    ## helpers
    Axx <- A %*% x
    Axn <- norm(A %*% x)
    error <- vector(length = iter)
    iters <- vector(length = iter)
 
    ## main loop
    for (i in 1:iter) {
        gradient_x <- t(A) %*% ( A %*% xx - y )
        xx_tmp <- xx - eta * gradient_x
        v <- eta * lambda
        # L1 prox/shrinkage-thresholding
        xx <- pmax(xx_tmp - v, 0) - pmax(- xx_tmp - v, 0)
        error[i] <- norm(A %*% xx - Axx) / Axn
        iters[i] <- i
    }
 
    return(list(xx, error, iters))
}
 
## FISTA
fista <- function(A, x, beta, iter = 100) {
    ## parameters
    eta <- 1 / beta
    lambda <- 1
    x_next <- c(0, 0, 0, 0, 0, 0)
    z_prev <- x_next
    z_next <- x_next
    mu_prev <- 0
    mu_next <- 0
    ## helpers
    Ax <- A %*% x
    Ax_norm <- norm(Ax)
    error <- vector(length = iter)
    iters <- vector(length = iter)
 
    ## main loop
    for (i in 1:iter) {
        mu_next <- 0.5 * (1 + sqrt(1 + 4 * mu_prev^2))
        gamma <- (1 - mu_prev) / mu_next
        gradient_x_n <- t(A) %*% ( A %*% x_next - y )
        z_tmp <- x_next - eta * gradient_x_n
        v <- eta * lambda
        # L1 prox/shrinkage-thresholding
        z_next <- pmax(z_tmp - v, 0) - pmax(- z_tmp - v, 0)
        x_next <- z_next + gamma * (z_prev - z_next)
        z_prev <- z_next
        mu_prev <- mu_next
        error[i] <- norm(A %*% x_next - Ax) / Ax_norm
        iters[i] <- i
    }
 
    return(list(x_next, error, iters))
}
 
max_iter <- 500;
beta <- norm(A, type="F")^2
 
res1 <- ista(A, x, beta, max_iter)
res2 <- fista(A, x, beta, max_iter)
 
plot(res1[[3]], res1[[2]], col = "red", xlab = "iterations", ylab = "error", type = 'l', lty = 1)
lines(res2[[3]], res2[[2]], col = "blue", type = 'l', lty = 1)


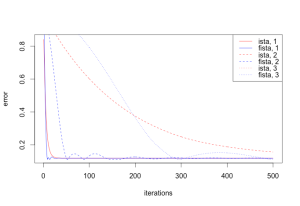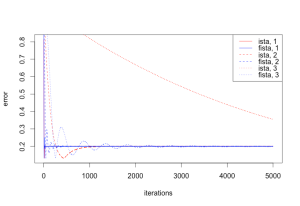ISTA vs FISTA, 500 iterations	5000 iterations

Note the non-monotonic convergence in FISTA’s case - [Beck09b, Teboulle10] describe a simple change to the algorithm to fix that. Another interesting problem with FISTA is the dependence on the worst-case smoothness parameter β in the algorithm, which can substantially reduce convergence rate for large β. This is addressed in [Katya14] using a backtracking strategy that to improve the dependence from worst-case to average “local composite Lipschitz constant for ∇f”, which can have a much smaller value, implying a larger step size. Another solution is presented in [Baes12].

Recall that ISTA, and hence FISTA, solve the following optimization problems:

$\min{( \frac{1}{2} \|Ax - b\|^2 +\lambda \|x\| )}$

FISTA works for non-smooth objectives as long as they can be formulated as the sum of a smooth and a non-smooth function [Section 2, Beck09; Section 3, Tseng08]. Are there efficient first-order algorithms for a larger class of non-smooth problems?

NESTA

NESTA Becker09 solves the following optimization problem that FISTA cannot since the objective function is non-composite non-smooth:

$\min{\|x\|_1} \mbox{s.t.} \|Ax - b\|_2 \le \epsilon$

This algorithm draws on [Nesterov05], which introduces a way to create smooth approximations of certain non-smooth function. This approximation, coupled with an accelerated gradient descent method, gives good convergence for optimizing a large class of non-smooth functions (though not as good as FISTA or Nesterov07). We’ll review [Nesterov05] via [Becker09] before returning to NESTA.

Smoothing non-smooth functions

Nesterov considers a class of functions that can be represented as [Section 2, [Nesterov05]; Section 2, Becker09; Nesterov08]

$\max_{u \in Q_d}\{(Ax - b)^{T}u - \phi{(u)}\}$

where $\phi{(u)}$ is a convex function and $Q_d$ is the dual domain (convex, closed) of a function $f(x)$ minimized over a domain $Q_p$. The representation is similar to the convex conjugate, $f^{\ast}(u)$, of this function. Indeed Nesterov considers using $\phi{(u)} = f^{\ast}(u)$, but then argues that such $\phi{(u)}$ might not be a simple enough function. This might be true in general, but as we’ll see that in the special case of $L_1$ regularization, $\phi{(u)} = f^{\ast}(u)$ will work.

Nesterov then presents a smooth approximation of the function

$f_{\mu}(x) = \max_{u \in Q_d}\{(Ax - b)^{T}u - \phi{(u)} - \mu\ prox_{\alpha}(u)\}$

where μ is the smoothness parameter, $prox_{\alpha}(u)$ is an $\alpha$-strongly convex proximal function over the dual domain $Q_d$. In the original paper [Nesterov05], Nesterov actually allows for a composite function approximation, that is $f(x) = fº(x) + f \mu{(x)}$ where $fº(x)$ is some smooth convex function. We’ll follow Becker09 in assuming that $fº(x) = 0$. Beck12 extends this smoothing framework to optimize an even broader class of non-smooth functions.

The important upshot is that (1) this function is smooth with factor $\frac{|A|}{\mu \alpha}$ [Theorem 1, [Nesterov05]], where $|A|$ is the operator norm of $A$, and (2) that $f_{\mu}(x)$ is a uniform smooth approximation of $f(x)$ for $\mu > 0$. So now we can use an optimal gradient descent for smooth optimization to minimize $f_{\mu}(x)$.

Smooth optimization

Section 3 in [Nesterov05] describes an optimal first-order algorithm to minimize a $\beta$-smooth convex function $f(x)$ using an $\alpha$-strongly convex proximal function $prox_{\alpha}(x)$.

$y_k = \mathrm{argmin}_{y}(\nabla{f(x_k)}^{T} + \frac{1}{2}\beta \|y - x_k\|^2)) \\ z_k=\mathrm{argmin}_{x}(\frac{\beta}{\alpha}\ prox_{\alpha}(x)+\sum_{i=0}^{k}(\frac{i+1}{2}[\nabla{f(x_i)} + \nabla{f(x_i)}^{T}(x - x_i)])) \\ x_{k+1} = \frac{2}{k+1}z_k + \frac{k+1}{k+3}y_k$

This is shown Theorem 2, [Nesterov05] to converge at a rate

$f(y_k) - f(x^\ast) \le \frac{4 \beta\ prox_{\alpha}(x^\ast)}{\alpha (k+1)(k+2)}$

This algorithm is more complicated than the earlier ones Nesterov83, Nesterov88 - especially when compared to the version FISTA uses (see previous post). The only advantage seems to be a somewhat better convergence rate by a factor of α at the cost of solving two minimization problems (instead of one as in FISTA).

Applying this algorithm to optimize $f_{\mu}(x)$ Theorem 3, [Nesterov05] gives $O(1/k)$ convergence for the optimal value of $\mu$ since:

$f(y_k) - f(x^\ast) \le O(1)\mu + \frac{O(1)}{\mu (k+1)^2} + \frac{O(1)}{(k+1)^2}$

Nesterov’s Algorithm

[Becker09] call their application of [Nesterov05] to $L_1$ regularization, NESTA. They show that:

(1) Optimizing over the convex conjugate of $L_1$ norm when combined with an appropriate proximal function yields a simple, well-known function called the Huber loss function. It is analytic and can be computed very efficiently, which makes it trivial to implement gradient descent (quite like the shrinkage-thresholding operation in ISTA/FISTA).

$\|x\| = \max_{u \in Q_d} \{(u^{T}x)\} \mbox{ where } Q_d = \{u : \|u\|_{\infty} \le 1\}$

Choosing $prox_{\alpha}(u)$ to be the squared Euclidean distance with $\alpha = 1$ (cf. Section 4.2, [Nesterov05]),

$f_{\mu}(x) = \max_{u \in Q_d}{(u^{T}x) - \frac{\mu}{2}|u|_2^2} = \begin{cases}\frac{x^2}{2\mu}, & |x| < \mu \ |x| - \frac{\mu}{2}, & otherwise\end{cases} $

$\nabla{f(x)[i]} = \begin{cases}\frac{x[i]}{\mu}, & |x[i]| < \mu \ sgn(x[i]), & otherwise\end{cases}$

(2) $y_k$ and $z_k$ updates in the original algorithm need to be modified taking into account the $L_2$ constraint. This is done using the Lagrangian form of each minimization that, under certain assumptions, allows expressing Lagrangian variables in terms of $\epsilon$.

(3) Another interesting idea is the use of “continuation.” Starting with a large value of the smoothing parameter and multiplicatively decreasing after each iteration helps converge more quickly (although the theoretical convergence rate stays the same).

Here’s R code for the unconstrained version of NESTA based on FISTA’s version of accelerated gradient descent:

nesta <- function(A, x, beta, iter = 100) {
    ## parameters
    eta <- 1 / beta
    lambda <- 1
    x_next <- c(0, 0, 0, 0, 0, 0)
    z_prev <- x_next
    z_next <- x_next
    mu_prev <- 0
    mu_next <- 0
    smooth <- 0.9 * norm(A, &quot;I&quot;)
    ## helpers
    Ax <- A %*% x
    Ax_norm <- norm(Ax)
    error <- vector(length = iter)
    iters <- vector(length = iter)
 
    ## main loop
    for (i in 1:iter) {
        mu_next <- 0.5 * (1 + sqrt(1 + 4 * mu_prev^2))
        gamma <- (1 - mu_prev) / mu_next
        # grad_huber1 + grad_huber2 = gradient of Huber function
        grad_huber1 <- (abs(x_next) &lt; smooth) / smooth
        grad_huber2 <- (abs(x_next) &gt;= smooth) * ifelse(x_next==0, 0, (x_next / abs(x_next)))
        gradient_x_n <- t(A) %*% ( A %*% x_next - y ) + grad_huber1 + grad_huber2
        z_next <- x_next - eta * gradient_x_n
        x_next <- z_next + gamma * (z_prev - z_next)
        z_prev <- z_next
        mu_prev <- mu_next
        smooth <- 0.5 * smooth
        error[i] <- norm(A %*% x_next - Ax) / Ax_norm
        iters[i] <- i
    }
 
    return(list(x_next, error, iters))
}

Postscript 02/09/2014

Building on the message-passing (aka belief propagation) algorithms introduced in [Donoho09], [Mousavi13] improve the convergence rate of iterative-shrinkage thresholding algorithm (ISTA) to $O(e^{-t})$. This was made possible by finding the optimal values of the regularization parameter, λ, at each iteration under the assumption of Gaussian error distribution (which is probably why it escapes the upper-bounds for first-order methods).

References

Baes12 M. Baes, M. Burgisser. An acceleration procedure for optimal first-order methods. 2012
Beck09 A. Beck, M. Teboulle. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM Journal of Imaging Sciences, 2009
Beck09b A. Beck, M. Teboulle. Fast Gradient-Based Algorithms for Constrained Total Variation Image Denoising and Deblurring Problems. IEEE Transactions on Image Processing, 2009.
Beck12 A. Beck, M. Teboulle. Smoothing and First Order Methods: A Unified Approach. SIAM Journal of Optimization, 2012.
Becker09 S. Becker, J. Bobin, E. Candes. NESTA: A Fast and Accurate First-Order Method for Sparse Recovery. Technical Report, Caltech, 2009
Bubeck14 S. Bubeck, Theory of Convex Optimization for Machine Learning
Donoho09 D. Donoho, A. Maleki, A. Montanari. Message-passing algorithms for compressed sensing. Proceedings of National Academy of Sciences, 2009.
Mousavi13 A. Mousavi, A. Maleki, R. Baranuick. Parameterless optimal approximate message passing. CoRR, 2013
[Nesterov83] Y. Nesterov. A method for solving a convex programming problem with convergence rate O(1/k2). Dokaldy AN SSR, 1983
[Nesterov88] Y. Nesterov. On an approach to the construction of optimal methods of minimization of smooth convex functions. Ekonom. i. Mat. Metody, 1988
[Nesterov04] Y. Nesterov. Introductory Lectures On Convex Programming: A Basic Course. Kluwer Academic Publishers, 2004
Nesterov05 Y. Nesterov. Smooth minimization of non-smooth functions. Mathematical Programming, 2005.
Nesterov07 Y. Nesterov. Gradient methods for minimizing composite objective function. Report, CORE, 2007
Nesterov08 Y. Nesterov. How to advance in Structural Convex Optimization. Optima, 2008
Katya14 K. Scheinberg, D. Goldfarb, X. Bai. Fast First-Order Methods for Composite Convex Optimization with Backtracking. Foundations of Computational Mathematics, 2014.
Teboulle10. M. Teboulle. First-Order Methods for Optimization. IPAM Optimization Tutorials, 2010
Tseng08 P. Tseng. On Accelerated Proximal Gradient Algorithms for Convex-Concave Optimization. SIAM Journal of Optimization, 2008

Implementations

Credits

Main image from lossfunctions.tumblr.

Posted by Umayr Hassan