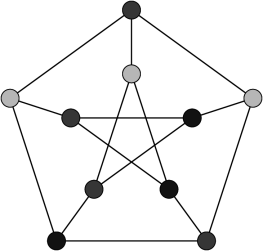
2-butterfly derangement
The hallmark of the Cooley-Tukey algorithm for
Fast Fourier Transform is the butterfly network, which helps reduce O(n2) computations to O(nlogn). Butterflies are very special graphs entangled in routing [Arora], switching [Chung], shuffling [Yang], and mixing [Czumaj].
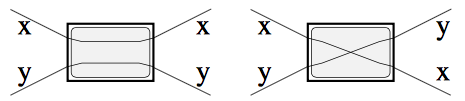
The butterfly with 2 inputs and outputs (aka radix-2 butterfly, or the bipartite graph K(2,2) is a building block for larger networks [Chung]. It can implement two distinct operations: pass-through and swap.
Problem 1: Can an array of size N be permuted using only swapping 2-butterflies in a single stage? Single stage implies that every element is swapped exactly once.
Clearly, it can be iff N is even (otherwise the mapping is not bijective). Each permutation is also a maximal matching on the K(N/2,N/2) spanning N elements.
Problem 2: Can an array be deranged using only swapping 2-butterflies in a single stage?
There are always at least two derangements for any even-sized array when N>2 (only one if N=2). One can be obtained by swapping N/2 non-overlapping pairs. Another, by swapping the two halves of the array. Here’re two for N=16:

Problem 3: How many such derangements are possible?
Let N=m∗2k, where m>=1 is some odd integer, and k>0. There are at most log(k) - or, log(N), if m=1 - distinct derangements.
Problem 4: Is there a permutation of the first N natural numbers, [1..N], such that if a number x is mapped to a number y in the permutation, then |x−y|==K for all x and y, and for a given 0<K<N? |.| denotes the absolute value. In other words, is there a bijective function f mapping [1..N] to [1..N] such that |x−f(x)|==K?

Since K > 0, this permutation must be a derangement. The previous two examples for N = 16 illustrate K = 1 and K = 8. They represent a derangement that swaps N / K groups of K neighbors with each other. If K leaves an even factor to N, and K <= N/2, then such a derangement always exists. Here’s a short program to print them out:
[code language=”java”] public static String permute(int n, int k) { StringBuilder result = new StringBuilder(2 * n); if (n % 2 == 0 && k > 0 && k <= (n / 2)) { // any k that leaves an even factor is fine // e.g. k = 4 for n = 12 is not valid but k = 2 is if ((n % k == 0) && ((n / k) % 2 == 0)) { // groups of k are swapped with neighbors int k2 = k * 2; for (int g = 0; g < n / k2; ++g) { int f = k2 * g; for (int i = k + 1; i <= k2; ++i) { result.append(f + i).append(“ “); } for (int i = 1; i <= k; ++i) { result.append(f + i).append(“ “); } } return result.toString(); } } return “No permutation exists”; } [/code]
- Arora S. Arora, F. T. Leighton, B. M. Maggs. Online algorithms for path selection in a nonblocking network.
- Chung F. R. K. Chung. An algebraic approach to switching networks.
- Yang Q. Yang, J. Ellis, K. Mamakani, F. Ruskey. In-place permuting and perfect shuffling using involutions.
- Czumaj A. Czumaj. Random permutations using __switching networks.