Maximum weighted independent set - connected component
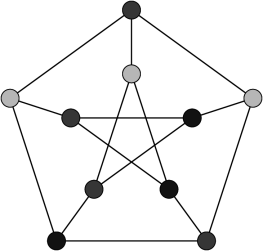
Given a weighted connected component, what is the weight of the maximum independent set, and how many different sets have this weight? A Petersen graph GP(5, 2) with zero vertex weights has three maximal subsets by size, 0 maximum set weight but 76 distinct independent sets with this weight.
The brute-force method is to enumerate all possible set of nodes, check for independence and filter for maximum weight. It is guaranteed to run 2^n times, which quickly becomes prohibitively slow (e.g. n >= 30). The only graph this method really works for is a forest of singletons, which, as we saw in the previous post, can be processed very quickly.
private static Result powerSetMethod(int size, Map<Integer, BitSet> adjacent, int[] compWeights) {
int maxSetSum = 0;
int maxSetCount = 0;
long maxIdx = (long) (Math.pow(2, size) - 1);
for (long idx = 1; idx <= maxIdx; ++idx) {
BitSet set = BitSet.valueOf(new long\[\] { idx });
if (isIndependent(set, adjacent)) {
int setSum = weightSum(set, compWeights);
if (setSum > maxSetSum) {
maxSetSum = setSum; maxSetCount = 1;
} else if (setSum == maxSetSum) {
++maxSetCount;
}
}
}
// number of ways to get the max weight
return new Result(maxSetSum, maxSetCount);
}
Yet, as we will see, it is still a simple and useful method for enumerating all sets if n is small.
A faster way would be to start with the set of all nodes and, in each iteration, check for independence. If the set is independent, check for the maximum weight. Otherwise, for a given node with conflict, create two new sets: one without the node, and one without its neighbors. The independent sets iteratively found this way are maximal.
/*
* select the node, v, from remnant component V that maximizes the values of w(v) + w(V - {v U N(v)}). V - {v U
* N(v)} is the remnant component for the next iteration.
*/
private static Result recursiveMethod(int size, Map<Integer, BitSet> adjacent, int[] compWeights) {
// all nodes to start with
BitSet maxSet = new BitSet(size);
maxSet.set(0, size);
TreeSet stack = new TreeSet<>(BITSET_COMPARATOR);
stack.add(maxSet);
return recurse(stack, adjacent, compWeights);
}
/**
* recursively find maximum weighted independent subset by enumerating all maximal independent subsets
*/
private static Result recurse(
TreeSet stack,
Map<Integer, BitSet> adjacent,
int[] compWeights
) {
HashSet maximalSets = new HashSet<>();
int maxSum = 0;
// collect maximal sets
while (!stack.isEmpty()) {
boolean isIndependent = true;
BitSet nodeSet = stack.pollFirst();
// for a pair of adjacents, create two new
for (int i = nodeSet.length(); (i = nodeSet.previousSetBit(i - 1)) >= 0;) {
BitSet adjSet = adjacent.get(i);
if (nodeSet.intersects(adjSet)) {
isIndependent = false;
BitSet newSet = (BitSet) nodeSet.clone();
newSet.clear(i); // keep neighbors
stack.add(newSet);
for (int j = adjSet.length(); (j = adjSet.previousSetBit(j - 1)) >= 0;) {
nodeSet.clear(j); // remove neighbors, reuse nodeSet
}
stack.add(nodeSet);
break;
}
}
if (isIndependent) {
int nodeSetSum = weightSum(nodeSet, compWeights);
if (nodeSetSum > maxSum) {
maxSum = nodeSetSum;
maximalSets.clear();
maximalSets.add(nodeSet);
} else if (nodeSetSum == maxSum) {
maximalSets.add(nodeSet);
}
}
}
// break maximal sets, if needed
HashSet indepSets = new HashSet<>();
for (BitSet nodeSet : maximalSets) {
processMaximalSet(nodeSet, compWeights, indepSets);
}
return new Result(maxSum, indepSets.size());
}
If all the nodes in a maximum independent set are positively weighted, we can just return all such sets. For maximum sets with zero-weighted nodes, we’ll need to find all unique subsets that have the same weight. This is where power-set enumeration is helpful.
private static void processMaximalSet(BitSet nodeSet, int[] compWeights, HashSet<Integer> indepSets) {
// generate and store all non-maximal independent subsets from a given maximal
List<Integer> nodesWithZeros = new ArrayList<>(nodeSet.length() + 1);
BitSet nodeSetClone = (BitSet) nodeSet.clone();
for (int i = nodeSet.length(); (i = nodeSet.previousSetBit(i - 1)) >= 0;) {
if (compWeights[i] == 0) {
nodesWithZeros.add(i);
nodeSetClone.clear(i);
}
}
if (nodesWithZeros.isEmpty()) {
indepSets.add(nodeSetClone.hashCode());
} else {
// no empty sets, please
if (nodeSetClone.cardinality() >= 1) {
indepSets.add(nodeSetClone.hashCode());
}
long maxIdx = (long) (Math.pow(2, nodesWithZeros.size()) - 1);
for (long idx = 1; idx <= maxIdx; ++idx) { BitSet idxSet = BitSet.valueOf(new long[] { idx }); BitSet cloneWithZeros = (BitSet) nodeSetClone.clone(); for (int i = idxSet.length(); (i = idxSet.previousSetBit(i - 1)) >= 0;) {
cloneWithZeros.set(nodesWithZeros.get(i));
}
indepSets.add(cloneWithZeros.hashCode());
}
}
}