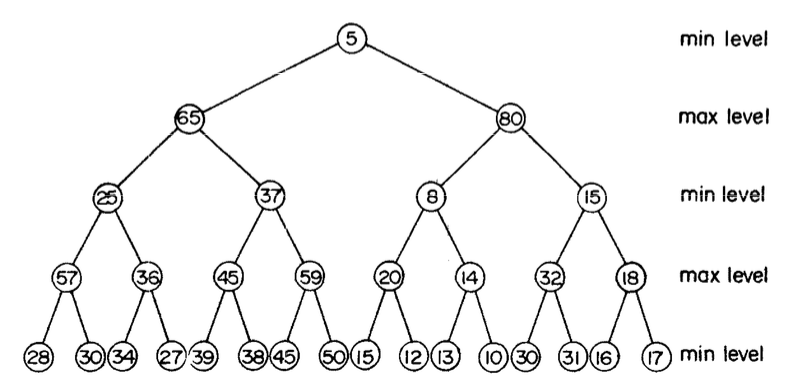
Min-max heaps were introduced in [ASSS86] as an efficient way to support heap operations for both minimum and maximum values. Structurally, the min-max heap levels alternate between min-heap condition and max-heap, and hence evaluates grandchildren/grandparents during insertion or search. Min-max heaps can also be generalized to find the k-th smallest element in $O(1)$ time.

An interesting application is finding the running median of a stream of numbers. [ASSS86] describe a simple extension called min-max-median heap that can find the running median in log-linear time complexity (indexed skip lists can too in amortized time complexity). The following code implements a method for finding the running median on each insertion. The trick is to maintain a min-max and a max-min heap such that either heap has at most one more element than the other.

public double add(int a) {
  if (minHeap.size() == 0) {
    minHeap.add(a);
    return a;
  }
  // add new element to appropriate heap
  if (a < minHeap.findMax()) {
      minHeap.add(a);
  } else {
      maxHeap.add(a);
  }
  int minSize = minHeap.size();
  int maxSize = maxHeap.size();
  // resize heaps to enforce size constraint
  if (maxSize == minSize - 2) {
      maxHeap.add(minHeap.removeMax());
  } else if (minSize == maxSize - 2) {
      minHeap.add(maxHeap.removeMin());
  }
  minSize = minHeap.size();
  maxSize = maxHeap.size();
  // calculate median
  if (minSize > maxSize) {
      return minHeap.findMax();
  } else if (maxSize > minSize) {
      return maxHeap.findMin();
  }
  return (minHeap.findMax() + maxHeap.findMin()) / 2.0;
}

ASSS86 M. D. Atkinson, J.-R. Sack, N. Santoro, and T. Strothotte. Min-max Heaps and Generalized Priority Queues. Communications of the ACM, Vol. 29 No. 10, 1986.