Three forecasting techniques
How well are we doing when forecasting for online ads at Adap.tv? Can we do better? To start answering such questions, I used R to experiment with three well-known forecasting techniques and used an hourly metric (transformed for data privacy) across all ads for seven days (Feb 1-Feb 7) as my training data set. Then I use each of the techniques to predict for the eight day (Feb 8), and compare the predicted values with actual data. Here’s a synopsis of the three:
Exponential Weighted Moving Average (EWMA)_
Strictly speaking, the smoothing filter that we currently use at Adap.tv for forecasting is not EWMA, but more like Weighted Moving Average. EWMA is defined by:
 (ref)
(ref)
So, if a = 0.9, S[t] = 0.9 ( y[t-1] + 0.1*y[t-2] + 0.01*y[3] … 1e-6*y[t-7]) would be an implementation of EWMA. Instead, our implementation is be: S[t] = 0.9 ( y[t-1] + 0.9*y[t-2] + 0.81*y[3] … 0.531441*y[t-7]) / (0.9+…). The critical difference is in the way past data is weighted - with EWMA data in remote past is heavily penalized, whereas, comparatively, in our implementation it is not.
Fig. 1 below shows a plot that forecasts our metric for Feb 8 using Weighted Moving Average akin to our implementation. The metric forecasted for Feb 8 was 68392533 whereas observed value was 63868927, giving an absolute difference of ~7.1%. The absolute hourly differences lie between 0.6-29%.
Fig. 1, “Weighted moving average” 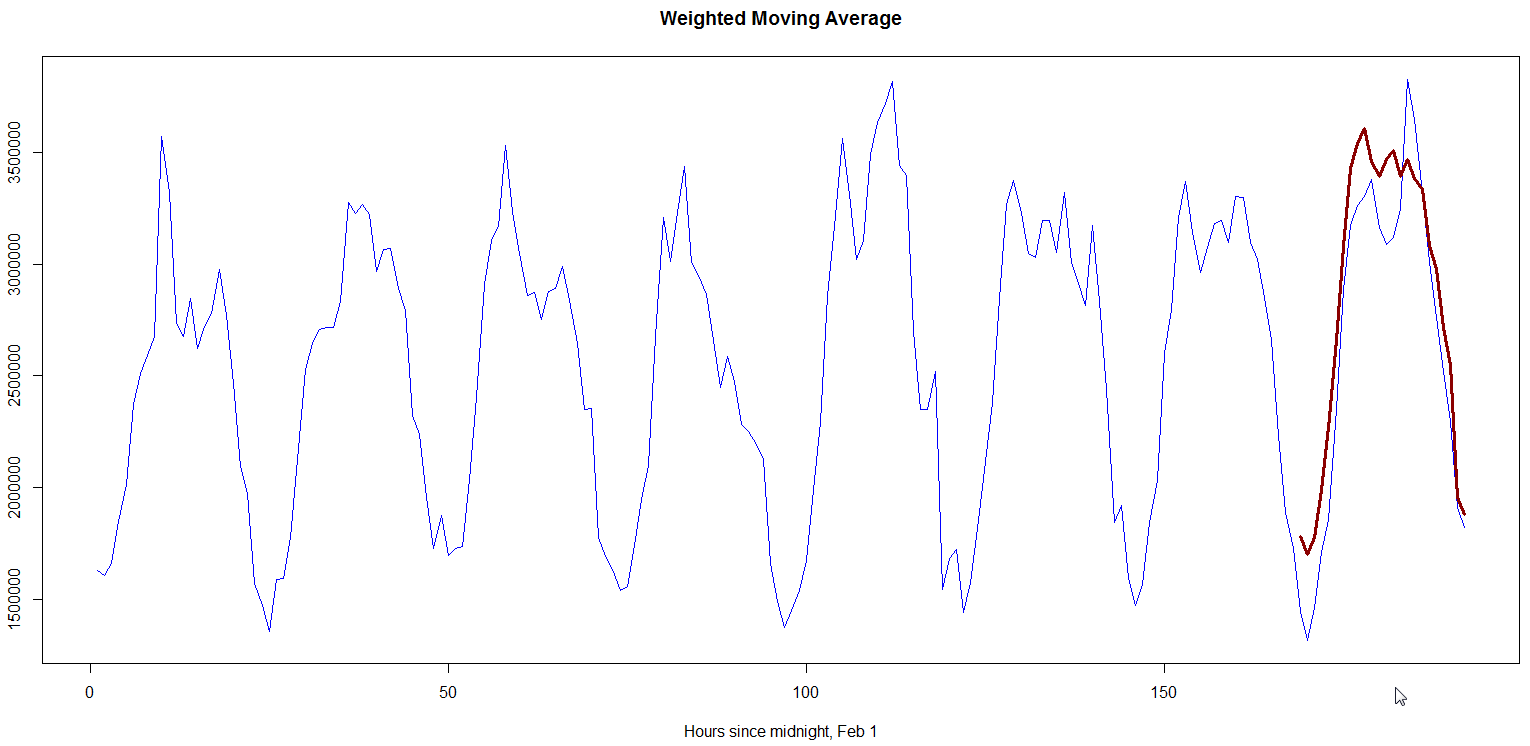
Harmonic regression_ Harmonic regression attempts to find the best-fitting periodic signals that can
characterize a time series. For example, we a time series may be represented by a linear sum of sinusoids:
![\frac{a_0}{2} + \sum_{n=1}^\infty \, [a_n \cos(nx) + b_n \sin(nx)]](http://upload.wikimedia.org/wikipedia/en/math/2/7/3/27359a25f09cb3722c2300b6daa9890e.png) (ref)
(ref)
Generally, a combination of Fourier transform and least-squares regression in used to find the harmonics who linear sum best fit training data. In my experiment, I used the top seven harmonics with highest power density (i.e. contribution to the model), and then used linear regression to find their amplitudes. Fig. 2 shows the model (in red) and actual data (in blue). The forecast for Feb 8 was 60476559 whereas the observed value was 63868927, giving an absolute difference of ~5.3%. The absolute hourly differences lie between 0.05-25%.
Fig. 2, “Harmonic regression” 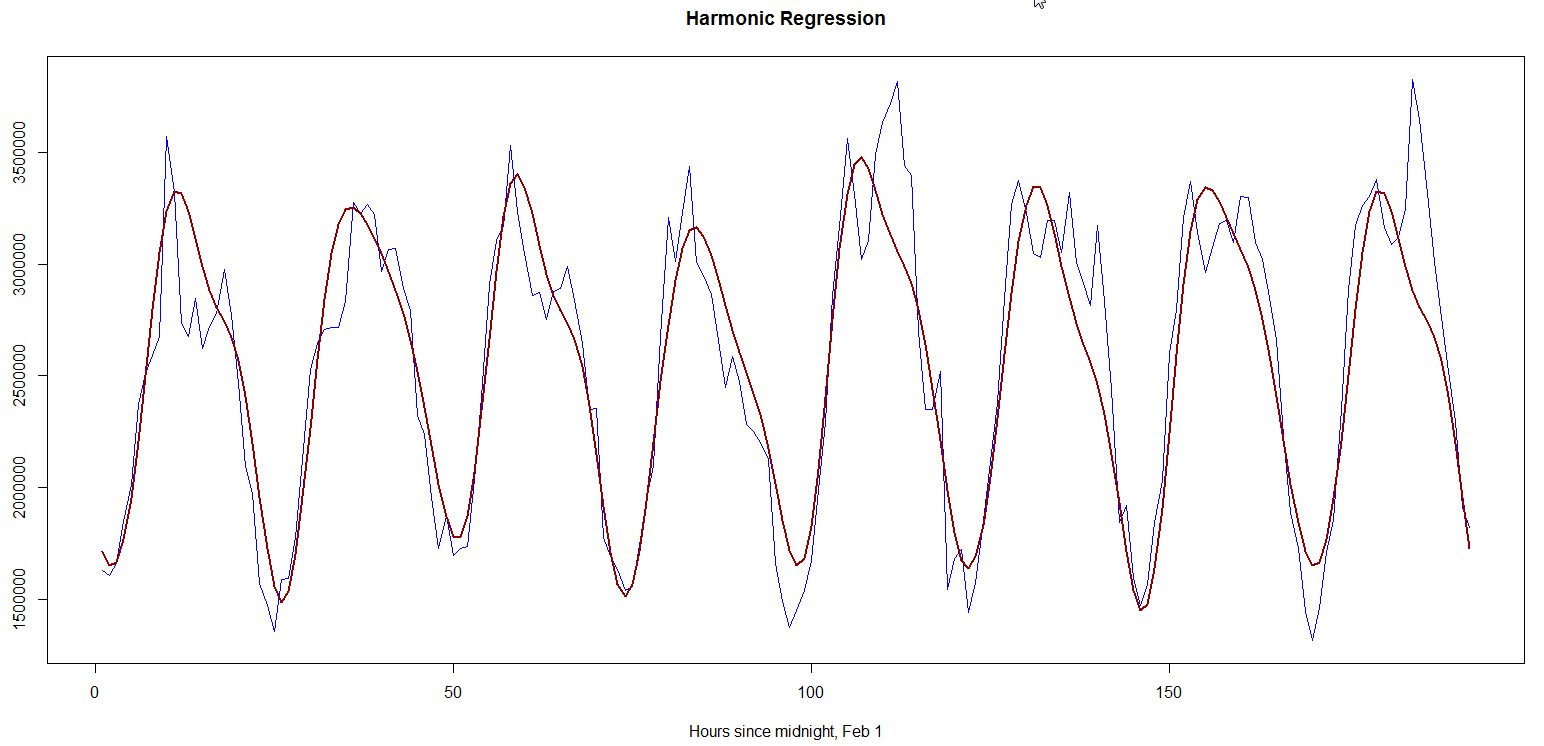 ](/assets/images/harmreg2.png)
](/assets/images/harmreg2.png)
Holt-Winters method_
Holt-Winters method augments EWMA to account for data trends and seasonality.
 (ref)
(ref)
The model I used assumes that the seasonal component is additive (instead of being multiplicative). Fig. 3 illustrates the breakdown of seasonality, trend and randomness in the data, Fig. 4 contrasts observed data with predicted data (note that the prediction start after one period, and the phase lag in predicted data), while Fig. 5 shows Holt-Winters prediction for Feb 8 versus observed data. The forecasted metric for Feb 8 was 63801332 whereas observed value was 63868927, giving an absolute difference of ~0.11%. The absolute hourly differences lie between 1.3-20%.
Fig. 3 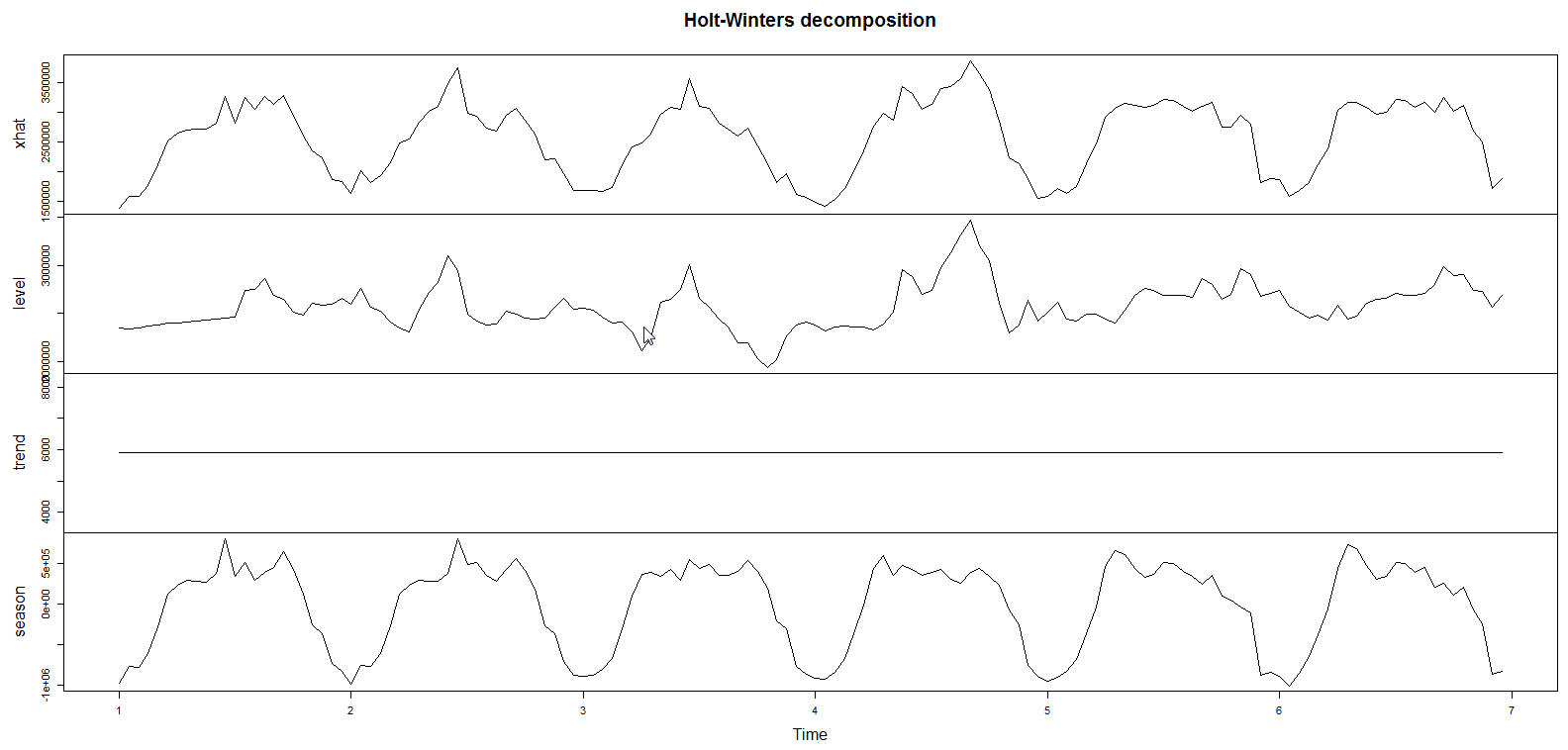 ](/assets/images/holtwintersdecomposition2.png)
](/assets/images/holtwintersdecomposition2.png)
Fig. 4 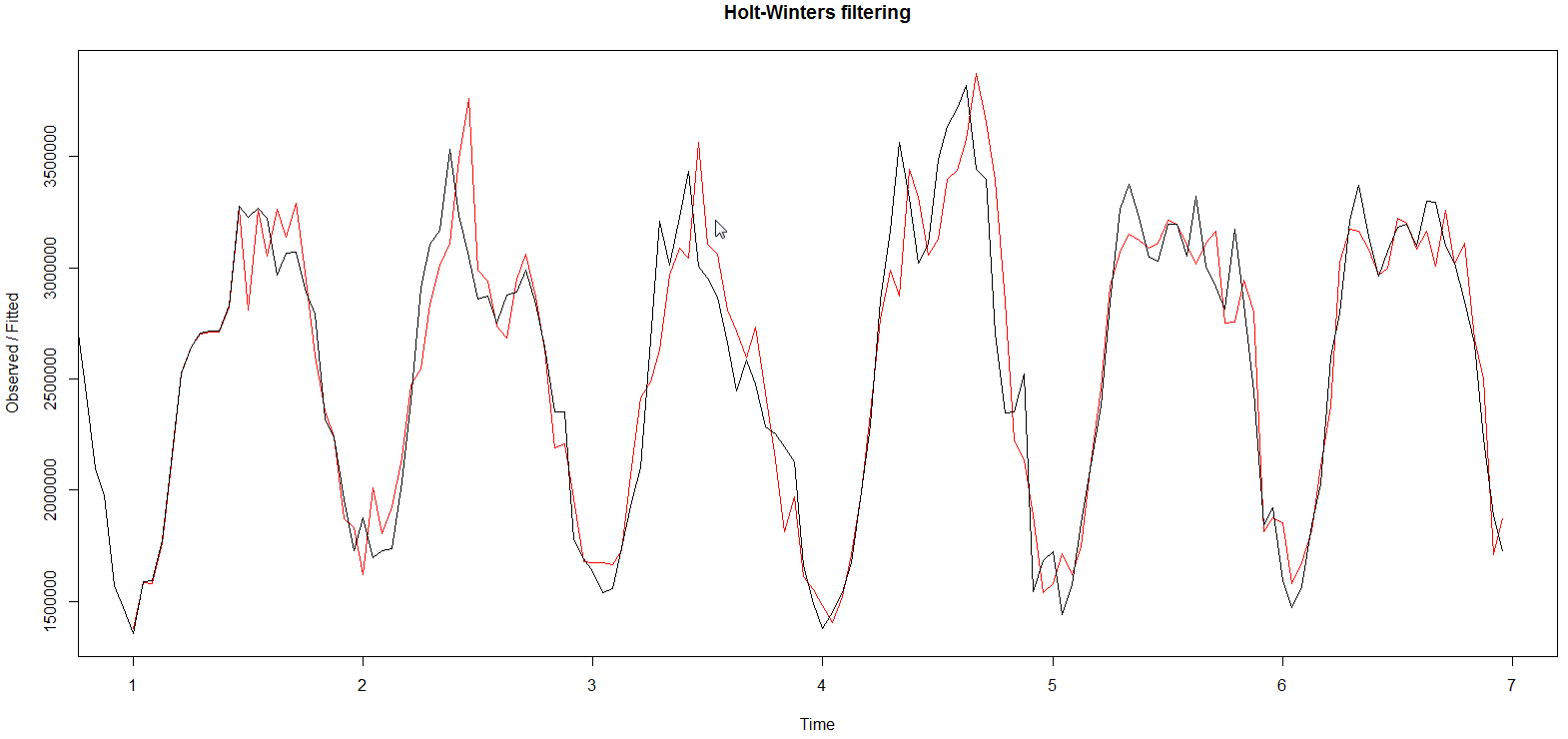 ](/assets/images/holtwintersfit2.png)
](/assets/images/holtwintersfit2.png)
Fig. 5 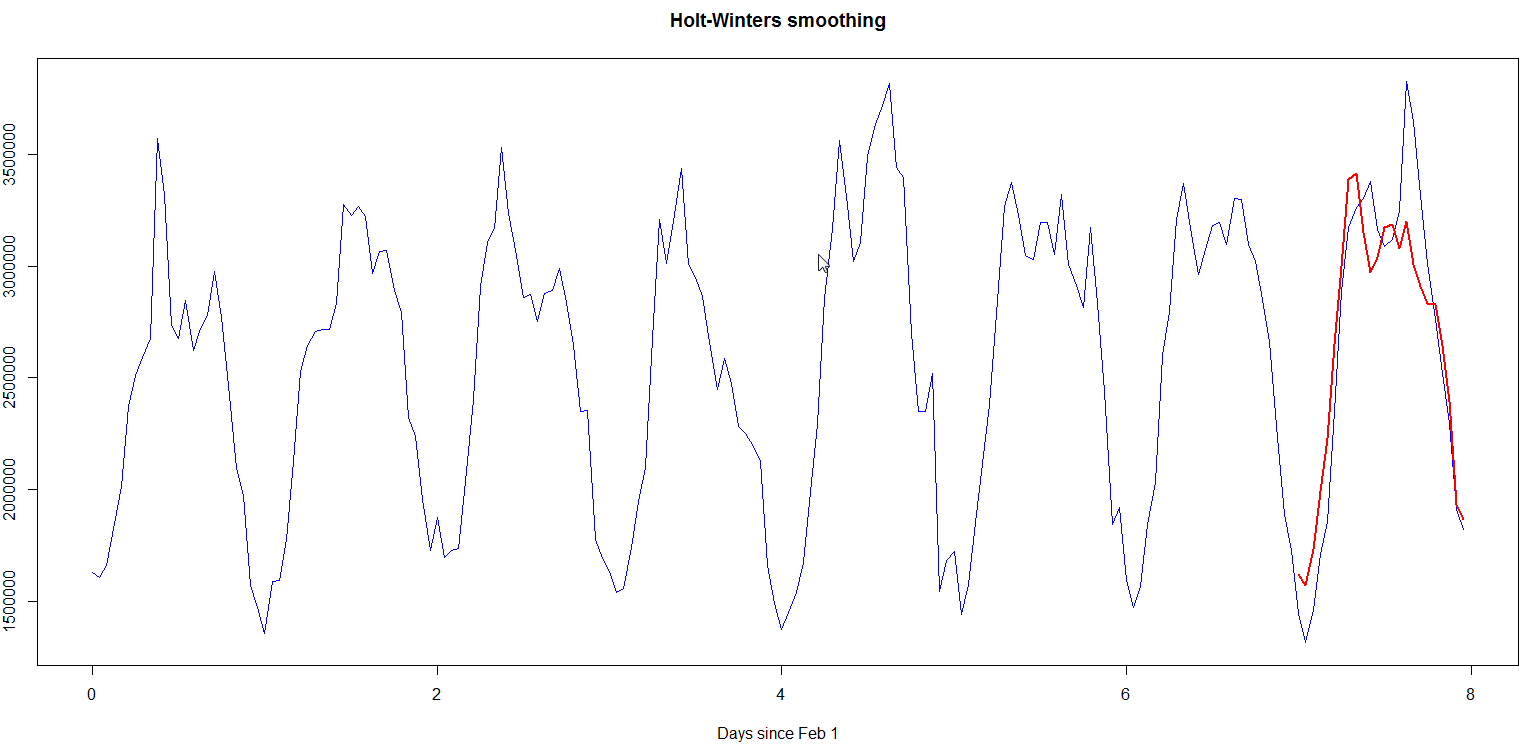 ](/assets/images/holtwintersprediction2.png)
](/assets/images/holtwintersprediction2.png)
TO-DO
- Compare these models for other data set time ranges (weeks, months, quarters)
- Compare these models for other metrics by sub-populations (e.g. by view domains)
- Test for stationarity, or otherwise heteroscedasticity, across models and data sets. This may be critical since non-stationary time series should not be modeled with moving average methods
- Compare models when data is uniformly sampled